Today to organize the top ten classic sorting algorithms.
1.Bubbling sort
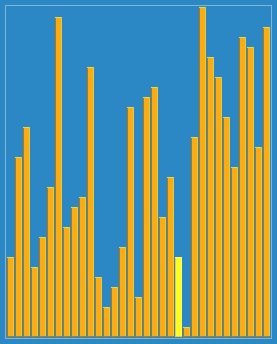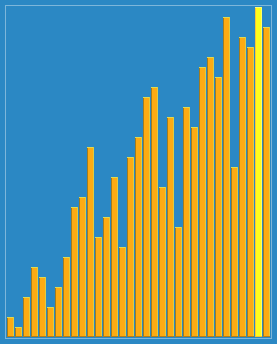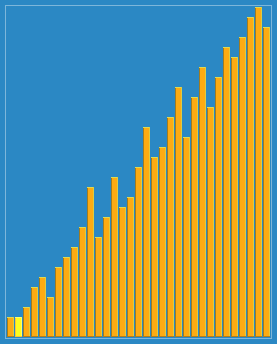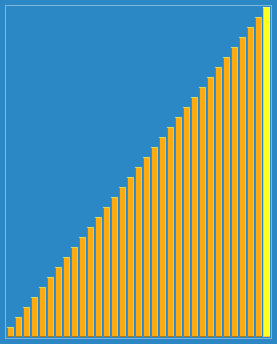
The smaller the elements will be slowly “floated” to the top of the array by swapping
Algorithm demonstration:
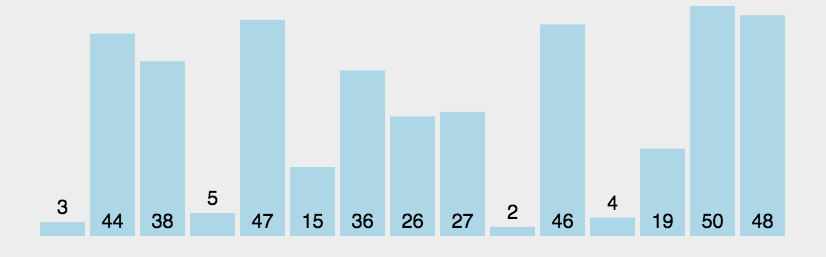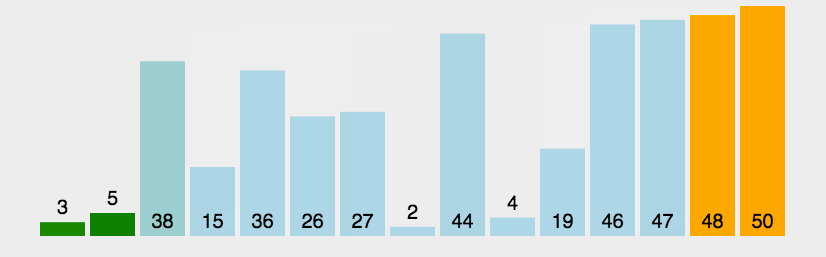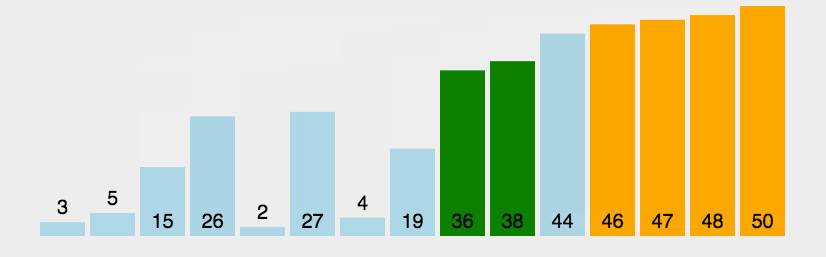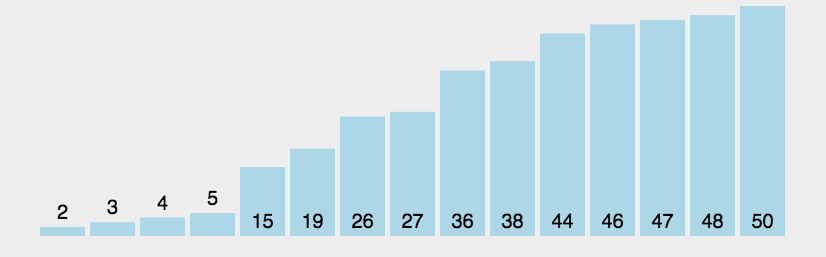
Algorithm steps:
- Compare adjacent elements. If the first is larger than the second, swap them both.
- Do the same for each pair of adjacent elements, from the first pair at the beginning to the last pair at the end, so that the element at the end should be the largest number.
- Repeat the above steps for all elements except the last one.
- Repeat steps 1 to 3 until the sorting is complete.
Algorithm Implementation:

2.Select Sort
The smallest comes out first, the second smallest comes out second…
Algorithm demonstration:
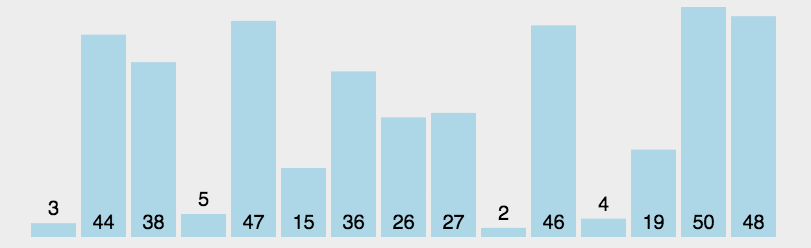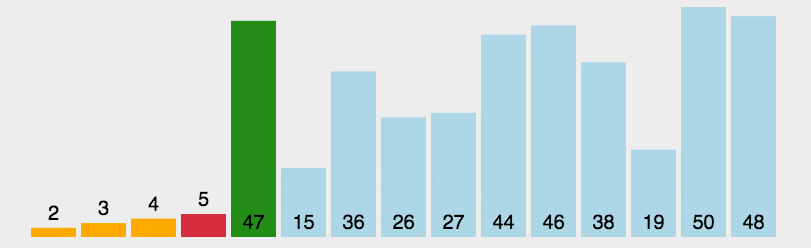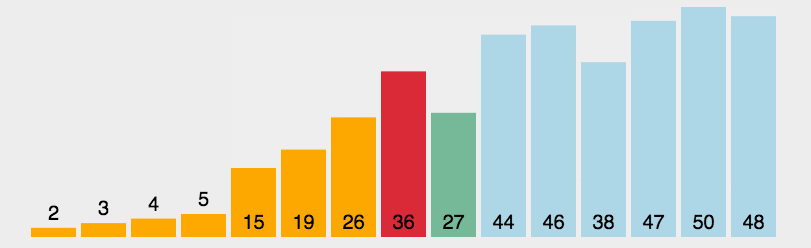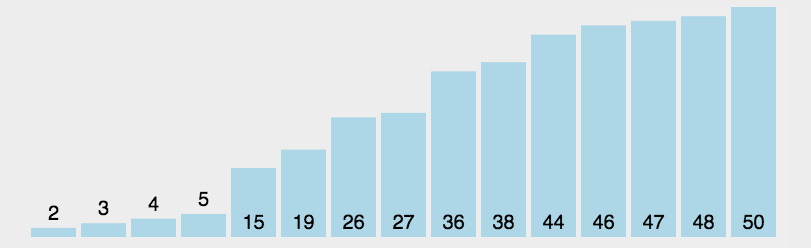
Algorithm steps:
- First, find the smallest (large) element in the unsorted sequence and store it at the beginning of the sorted sequence.
- Then find the smallest (large) element from the remaining unsorted elements and put it at the end of the sorted sequence.
- Repeat the second step until all elements are sorted.
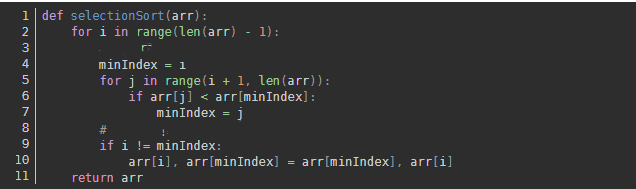
Algorithm Implementation:
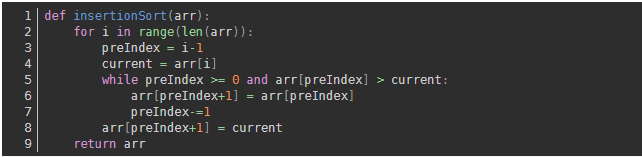
3. Simple insertion sort
By constructing an ordered sequence, the unsorted data is scanned from back to front in the sorted sequence, and the corresponding position is found and inserted.
Algorithm demonstration:
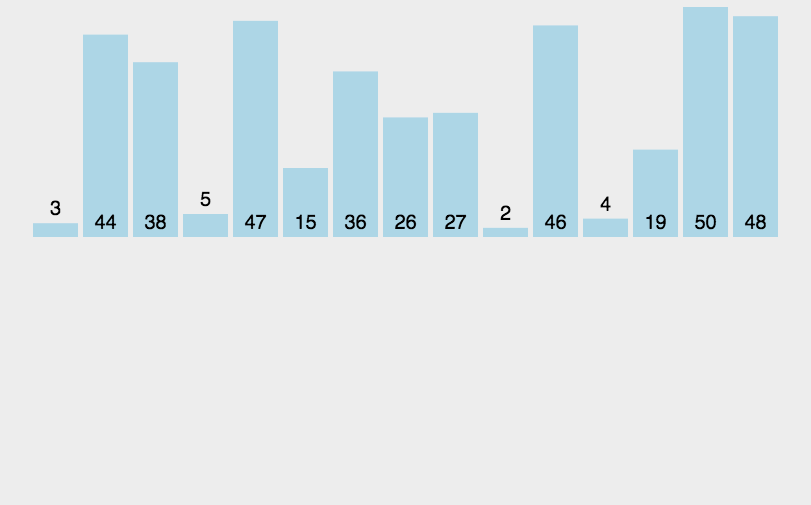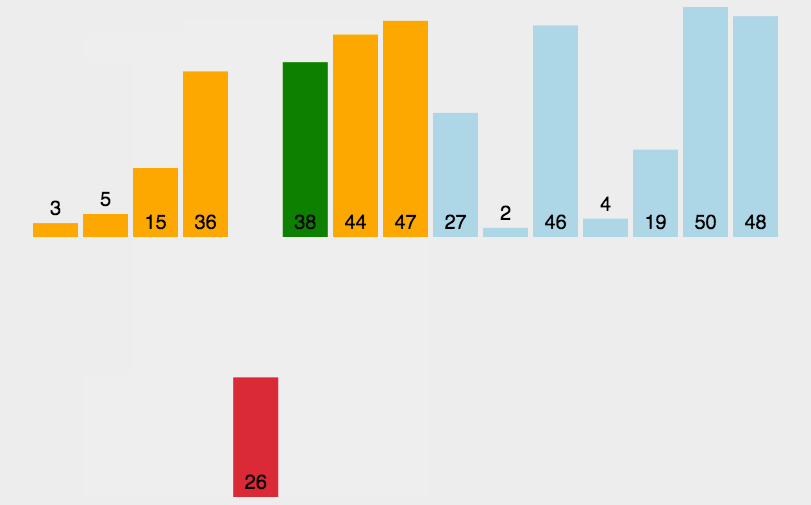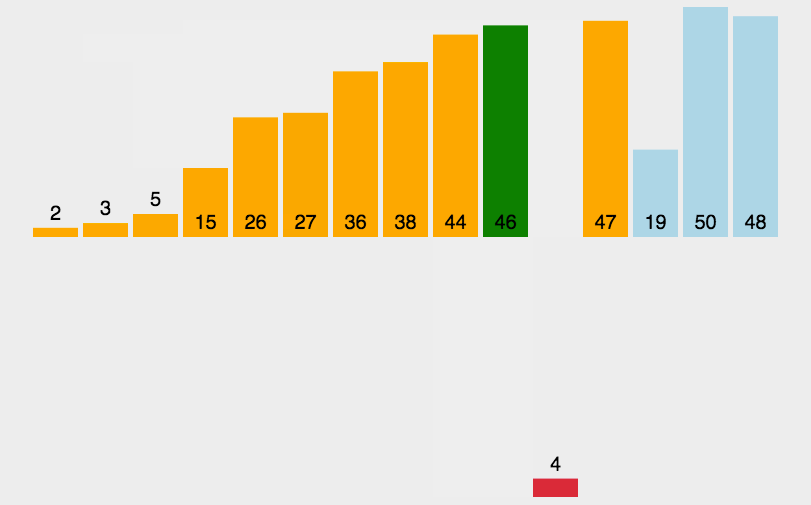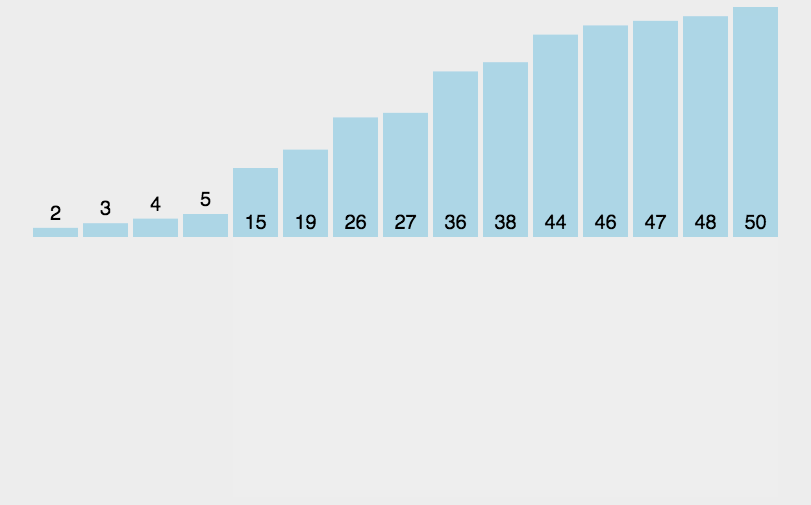
Algorithm steps:
- Starting with the first element, which can be considered to have been sorted.
- Taking the next element and scanning it backwards and forwards in the sequence of already sorted elements.
- If the element (already sorted) is larger than the new element, move the element to the next position.
- Repeating step 3 until a position is found where the sorted element is less than or equal to the new element.
- Inserting the new element after that position.
- Repeat steps 2 to 5.
Algorithm Implementation:
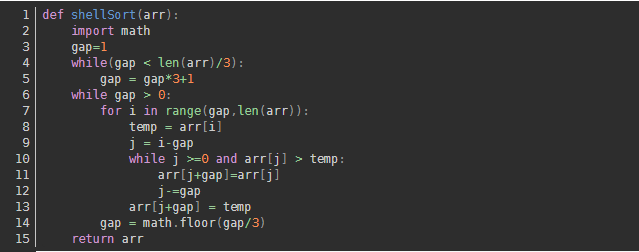
4.Hill Sort
Hill sort, also known as decreasing incremental sorting algorithm, is a more efficient and improved version of insertion sort.
Algorithm Demonstration:

Algorithm steps:
- Select an incremental sequence t1, t2, ……, tk, where ti > tj, tk = 1.
- Sort the sequence k times by the number of incremental sequences k.
- For each sort, according to the corresponding increment ti, the sequence to be sorted is partitioned into a number of subsequences of length m, and a direct insertion sort is performed on each sub-table respectively. Only when the increment factor is 1, the whole sequence is treated as a table, and the length of the table is the length of the whole sequence.
Algorithm Implementation:
5.Sorting by imputation
An efficient sorting algorithm built on the merge operation. This algorithm is a very typical application of the Divide and Conquer method.
Algorithm demonstration:
Algorithm steps:
- Requesting a space so that its size is the sum of the two already sorted sequences, which is used to store the merged sequence.
- Set two pointers, the initial position of which is the starting position of each of the two already sorted sequences.
- Compare the elements pointed by the two pointers, select the relatively small element to be put into the merged space, and move the pointer to the next position.
- Repeat step 3 until a pointer reaches the end of the sequence.
- Copy all the remaining elements of the other sequence directly to the end of the merged sequence.
Algorithm implementation:
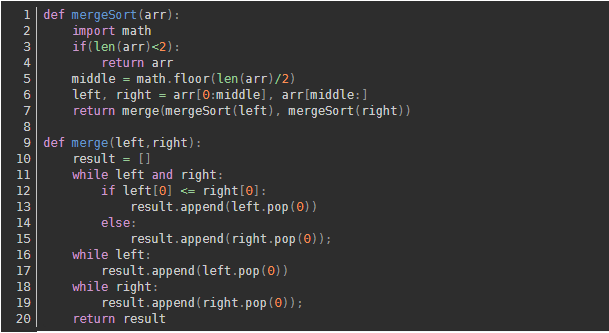
6.Fast sorting
Fast sort uses the Divide and conquer strategy to divide a serial (list) into two sub-lists. Quick sort is another typical application of the divide and conquer idea in sorting algorithms. Essentially, quick sort is a recursive partitioning method based on bubble sort.
Algorithm demonstration:
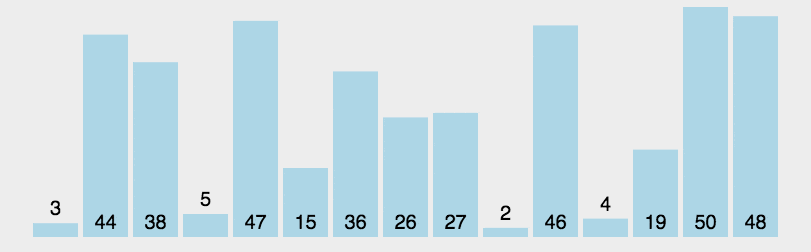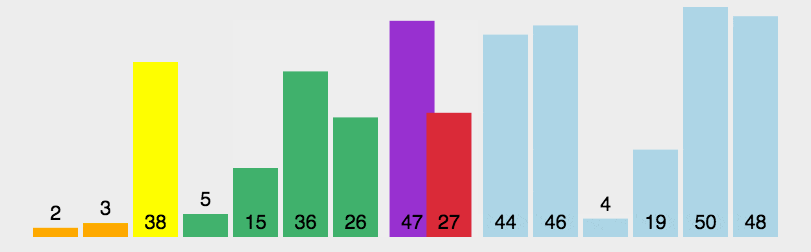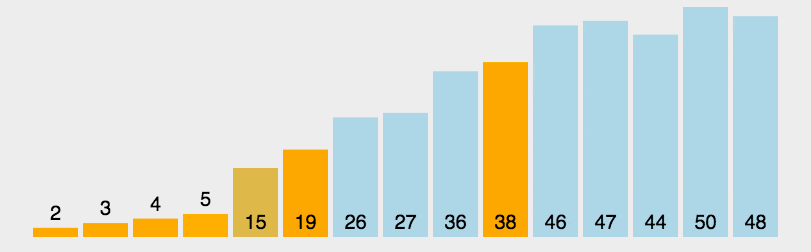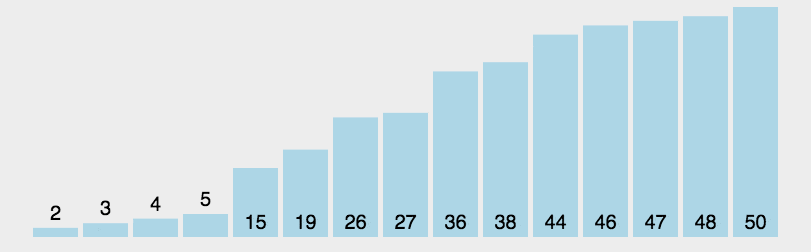
Algorithm steps:
- Pick an element from the series, called the “benchmark” (pivot);
- Reorder the series, with all elements smaller than the benchmark value placed in front of the benchmark, and all elements larger than the benchmark value placed behind the benchmark (the same number can go to either side). After this partition is exited, the benchmark is in the middle of the series. This is called a partition operation.
- Recursively sorting the subseries of elements smaller than the base and the subseries of elements larger than the base.
Algorithm Implementation:
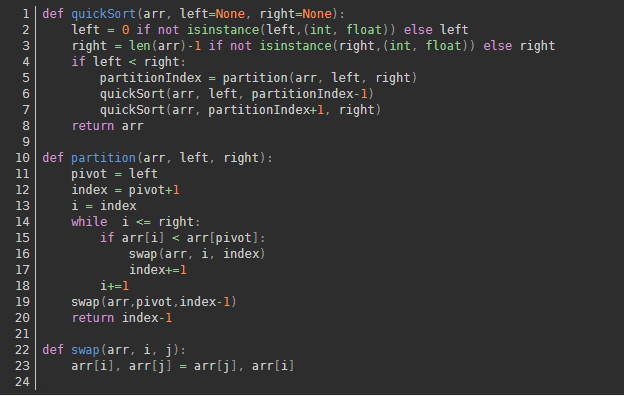
7.Heap sort
A sorting algorithm designed by using a data structure like a heap
Algorithm demonstration:

Algorithm steps:
- Create a heap H[0……n-1].
- Swap the top of the heap (the maximum value) with the bottom of the heap.
- Reduce the size of the heap by 1 and call shift_down(0) with the purpose of resizing the new top of the array data to the corresponding position.
- Repeat step 2 until the size of the heap is 1.
Algorithm Implementation:
8.Counting sort
As a linear time complexity sort, counting sort requires that the input data must be integers with a defined range.
Algorithm Demonstration:
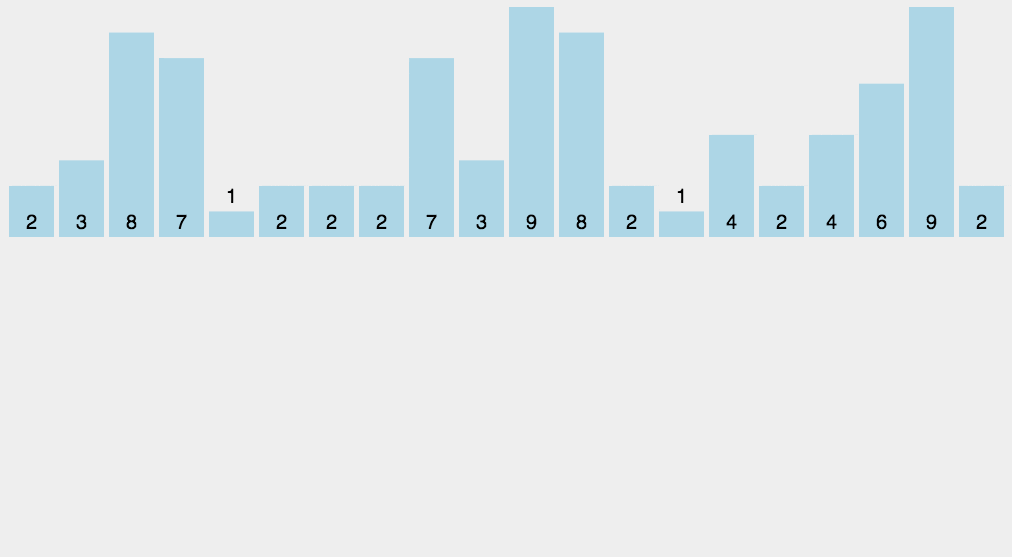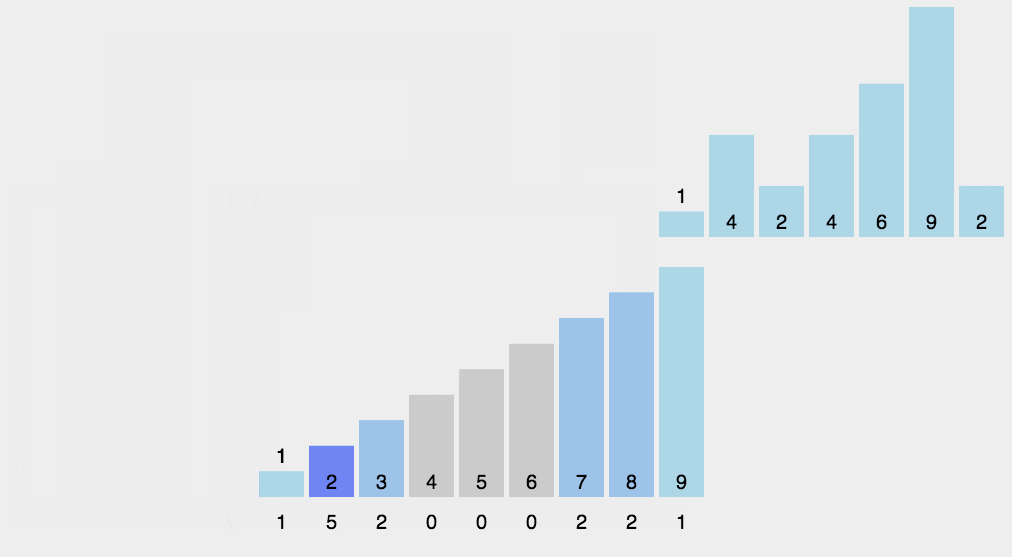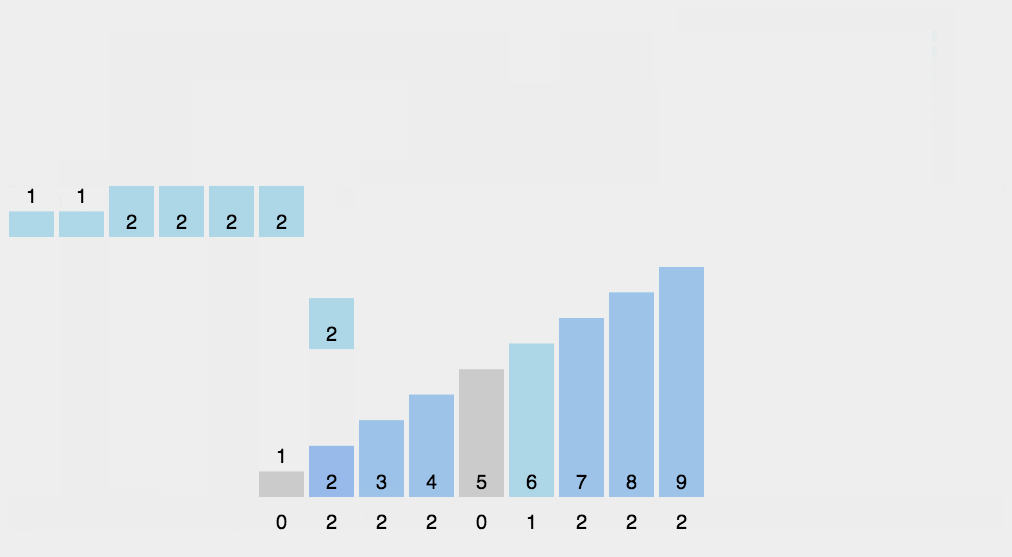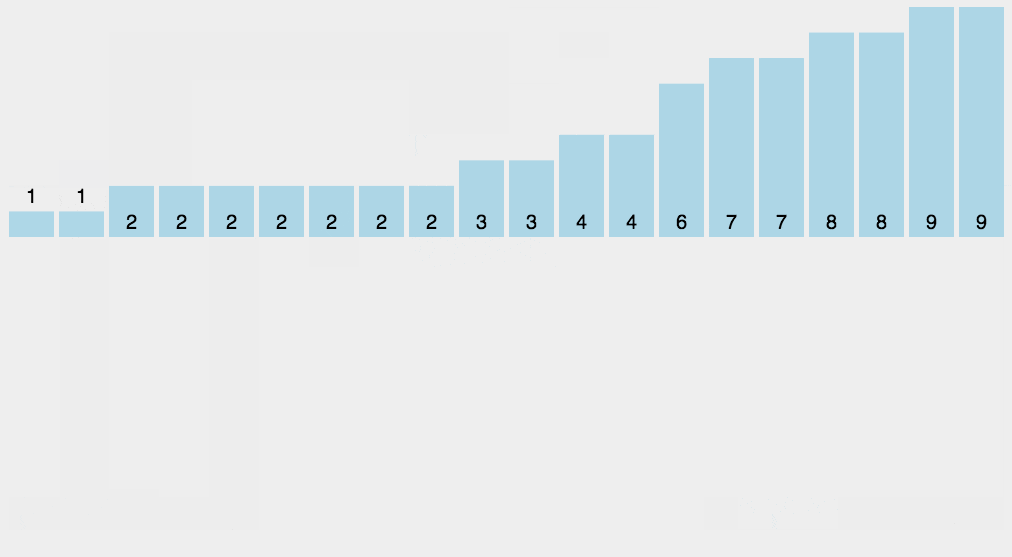
Algorithm steps:
- Find the largest and smallest elements of the array to be sorted.
- Count the number of occurrences of each element with value i in the array and store it in the i-th item of the array C.
- Add up all the counts (starting from the first element in C, each item is added to the previous one).
- Reverse fill the target array: place each element i in the new array at item C(i) and subtract 1 from C(i) for each element placed.
Algorithm implementation:
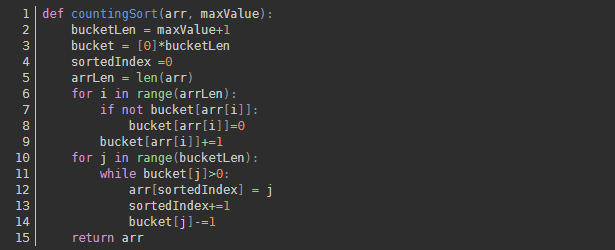
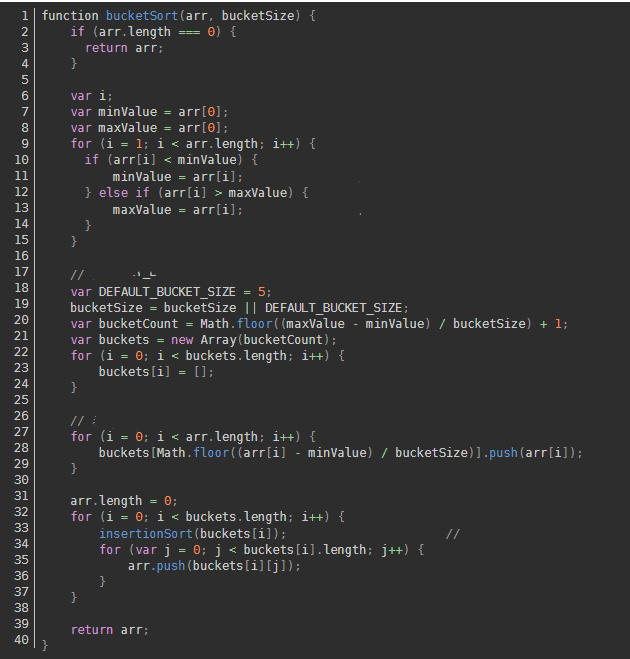
9.Bucket sort
Bucket sort is an upgraded version of counting sort. It uses the mapping relationship of functions, and the key to efficiency lies in the determination of this mapping function.
Algorithm demonstration:
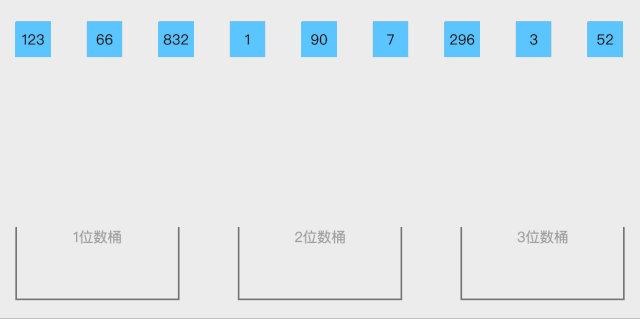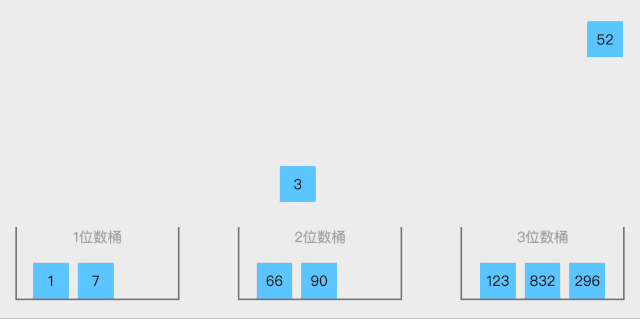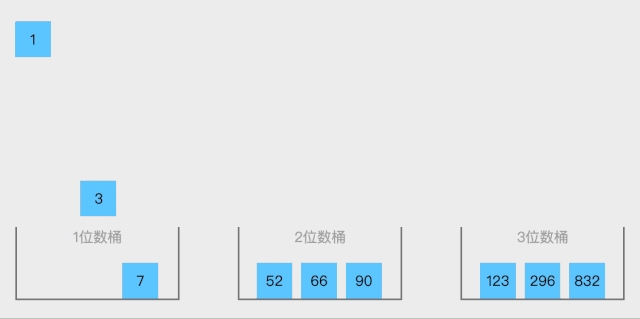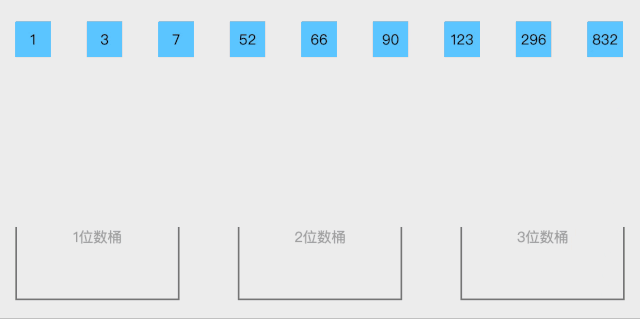
Algorithm steps:
- Setting up a quantitative array as an empty bucket.
- Traversing the input data and placing them one by one into the corresponding buckets.
- Sorting each bucket that is not empty.
- Piece together the sorted data from the buckets that are not empty.
Algorithm implementation;
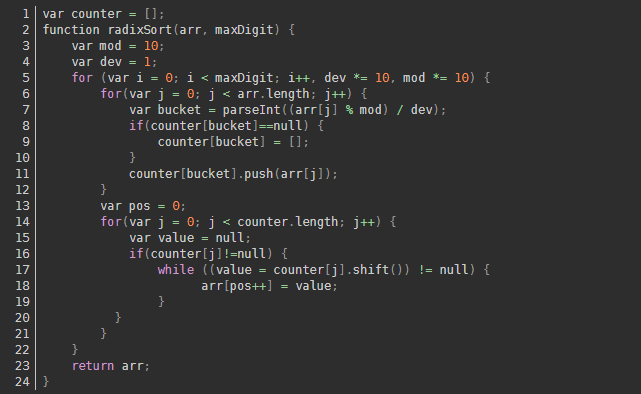
10.Base sorting
The base sort is sorted by low first, then collected; then sorted by high, then collected; and so on until the highest. Sometimes some attributes are in priority order, sorted by low priority first, then by high priority. The final order is that the high priority is first, and the low priority with the same high priority is first.
Algorithm demonstration:

Algorithm steps:
- Obtain the largest number in the array and obtain the number of bits.
- Arr is the original array, taking each bit from the lowest bit to form the radix array.
- Sorting the radix by counting (using the feature that counting sort is applicable to small ranges of numbers).
Algorithm implementation: