Algorithmic ideas are the core of problem solving, and 95% of all algorithms are based on these 6 algorithmic ideas, so let’s introduce these 6 algorithmic ideas to help you understand and solve various algorithmic problems.
1 Recursive algorithms
1.1 Algorithm strategy
A recursive algorithm is an algorithm that calls its own function or method directly or indirectly.
The essence of a recursive algorithm is to decompose a problem into smaller subproblems of the same kind, and then recursively invoke methods to represent the solution to the problem. Recursive algorithms are effective for solving a large class of problems, and they make the algorithm concise and easy to understand.
Advantages and disadvantages.
Pros: Simple to implement and easy to use
Disadvantages: recursive algorithm for common algorithms such as ordinary loops, operational efficiency is low; and in the process of recursive invocation of the system for each layer of the return point, local volume, etc. to open up a stack to store, recursion is too deep, easy to happen stack overflow
1.2 Applicable scenarios
Recursive algorithms are generally used to solve three types of problems.
The data is defined recursively. (Fibonacci sequence)
The problem solution is implemented by recursive algorithm. (backtracking)
The structural form of the data is defined recursively. (tree traversal, graph search)
Recursive problem solving strategy.
Step 1: clarify the input and output of your function, first regardless of what code is inside the function, but first understand, what is the input of your function, what is the output, what is the function, and what kind of a thing to accomplish.
Step 2: Find the recursion end condition, we need to find out when the recursion ends, and then directly return the results
Step 3: Clarify the recursive relational formula, how to solve the current problem by combining various recursive calls
1.3 Some classic problems solved using recursive algorithms
Fibonacci sequence
The Hanotah problem
Tree traversal and related operations
DOM tree as an example
The following is an implementation of document.getElementById using the DOM as an example
Since DOM is a tree, and the definition of tree itself is defined recursively, it is very simple and natural to use recursive method to deal with tree.
Step 1: Define the input and output of your function
Recursive from the DOM root node down to determine whether the current node id is the id=’d-cal’ we are looking for
Input: the DOM root document with the id=’d-cal’ we’re looking for
Output: return the child node that meets id=’sisteran’
function getElementById(node, id){}
Step 2: Find the recursive end condition
Starting from document and working down, recursively look for their child nodes for all child nodes, one level down.
If the id of the current node matches the search condition, return the current node
If the id of the current node matches the search condition, the current node is returned. If the leaf node is not found, null is returned.
function getElementById(node, id){
// If the current node does not exist and has reached the leaf node but has not been found, return null
if(!node) return null
// The id of the current node meets the search criteria, return the current node
if(node.id === id) return node
}
Step 3: Clarify the recursive relational formula
If the id of the current node does not meet the search criteria, recursively search for each of its child nodes
function getElementById(node, id){
// The current node does not exist, it has reached the leaf node and not found yet, return null
if(!node) return null
// The id of the current node meets the search criteria, return the current node
if(node.id === id) return node
// If the id of the previous node does not meet the search criteria, continue to search for each of its children
for(var i = 0; i < node.childNodes.length; i++){
// recursively find each of its child nodes
var found = getElementById(node.childNodes[i], id);
if(found) return found;
}
return null;
}
That’s it, one of our document.getElementById functions has been implemented.
function getElementById(node, id){
if(!node) return null;
if(node.id === id) return node;
for(var i = 0; i < node.childNodes.length; i++){
var found = getElementById(node.childNodes[i], id);
if(found) return found;
}
return null;
}
getElementById(document, “d-cal”);
The advantage of using recursion is that the code is simple and easy to understand, and the disadvantage is that the efficiency is not as good as the non-recursive implementation. chrome browser’s checking DOM is implemented using non-recursion. How to implement non-recursive?
The following code.
function getByElementId(node, id){
// Iterate through all the Nodes
while(node){
if(node.id === id) return node;
node = nextElement(node);
}
return null;
}
It still iterates through all the DOM nodes in turn, but this time it’s a while loop and the nextElement function is responsible for finding the next node. So the key is how this nextElement implements the non-recursive node finding function.
// deep traversal
function nextElement(node){
// first determine if there is a child node
if(node.children.length) {
// if there is, return the first child node
return node.children[0];
}
// then determine if there are neighboring nodes
if(node.nextElementSibling){
// return its next adjacent node if it does
return node.nextElementSibling;
}
// otherwise, return the next adjacent element of its parent node up, equivalent to i plus 1 in the for loop in the recursive implementation above
while(node.parentNode){
if(node.parentNode.nextElementSibling) { if(node.parentNode.nextElementSibling) {
return node.parentNode.nextElementSibling;
}
node = node.parentNode;
}
return null;
}
Running this code inside the console also outputs the results correctly. Whether non-recursive or recursive, they are both depth-first traversals, and the process is shown in the figure below.
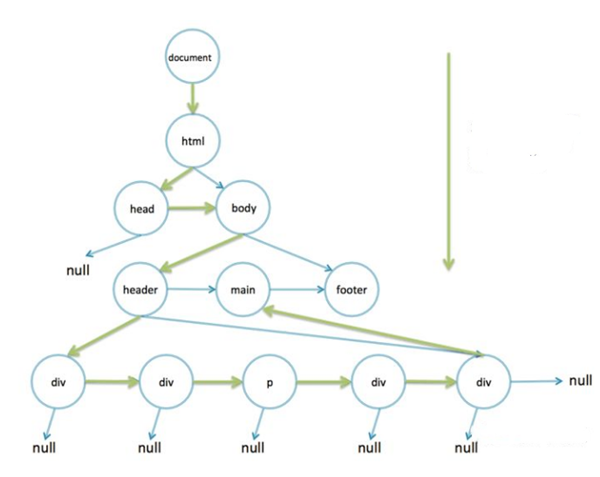
In fact, getElementById is stored in a hash map that maps directly to DOM nodes based on id, and getElementsByClassName is a non-recursive lookup like this.
Reference: Front-end data structures and algorithms I’ve come across
2. Partitioning algorithm
2.1 Algorithm strategy
In computer science, partitioning algorithm is a very important algorithm, fast sort, subsumption sort, etc. are based on partitioning strategy for implementation, so it is recommended to understand it.
Partitioning, as the name implies, is to divide and conquer a complex problem into two or more similar subproblems, and then divide the subproblem into smaller subproblems until the smaller subproblem can be solved simply by solving the subproblem, and then the solution of the original problem is a merge of the solutions of the subproblem.
2.2 Applicable scenarios
A partition-only strategy can be tried to solve the problem when the following conditions are satisfied.
The original problem can be divided into multiple similar subproblems
the subproblem can be solved very simply
The solution of the original problem is a merge of the subproblem solutions
The subproblems are independent of each other and do not contain the same subproblem
The solution strategy of partitioning.
Step 1: Decompose the original problem into several smaller, independent subproblems of the same form as the original problem
Step 2: Solve, solve each subproblem
Step 3: Merge, combining the solutions of each subproblem into the solution of the original problem
2.3 Some classical problems solved using partitioning method
Dichotomous lookup
Summation sort
Fast sorting
Hannota problem
React time slicing
Dichotomous lookup
Also known as the fold-and-half lookup algorithm, it is a simple and easy to understand fast lookup algorithm. For example, I write a random number between 0 and 100 and ask you to guess what I wrote. For each guess you make, I will tell you whether your guess is bigger or smaller until you get it right.
Step 1: Breakdown
Each time you guess, break up the previous result into a larger group and a smaller group, with the two groups being independent of each other
Select the middle number of the array
function binarySearch(items, item) {
// low, mid, high divide the array into two groups
var low = 0,
high = items.length – 1,
mid = Math.floor((low+high)/2),
elem = items[mid]
// …
}
Step 2: Solve the subproblem
Find the number versus the middle number
lower than the middle number, go to the subarray to the left of the middle number
higher than the middle number, go to the subarray to the right of the middle number.
If they are equal, the search is successful
while(low <= high) {
if(elem < item) { // higher than the middle number
low = mid + 1
} else if(elem > item) { // lower than the middle number
high = mid – 1
} else { // equal
return mid
}
}
Step 3: Merge
function binarySearch(items, item) {
var low = 0,
high = items.length – 1,
mid, elem
while(low <= high) {
mid = Math.floor((low+high)/2)
elem = items[mid]
if(elem < item) {
low = mid + 1
} else if(elem > item) {
high = mid – 1
} else {
return mid
}
}
return -1
}
Finally, binary search can only be applied to ordered arrays, if the array is unordered, binary search won’t work
function binarySearch(items, item) {
// quickSort
quickSort(items)
var low = 0,
high = items.length – 1,
mid, elem
while(low <= high) {
mid = Math.floor((low+high)/2)
elem = items[mid]
if(elem < item) {
low = mid + 1
} else if(elem > item) {
high = mid – 1
} else {
return mid
}
}
return -1
}
// Test
var arr = [2,3,1,4]
binarySearch(arr, 3)
// 2
binarySearch(arr, 5)
// -1
3 Greedy Algorithm
3.1 Algorithm strategy
A greedy algorithm, as the name implies, always makes the current optimal choice, i.e., it expects to obtain the overall optimal choice through the local optimal choice.
In a sense, the greedy algorithm is very greedy and short-sighted, it does not consider the whole, but only focus on the current maximum benefit, so that it makes the choice is only a sense of the local optimal, but the greedy algorithm in many problems can still get the optimal solution or better solution, so its existence is still meaningful.
3.2 Application Scenarios
In daily life, we use the greedy algorithm quite often, for example
How can we get the most value out of 10 bills of varying denominations drawn from 100 chapters?
We just need to choose the largest denomination of the remaining bills each time, and the last one we must get is the optimal solution, which is the greedy algorithm used, and finally we get the overall optimal solution.
However, we still need to be clear that the expectation that the overall optimal choice will be obtained through the local optimal choice is just an expectation, and the final result may not necessarily be the overall optimal solution.
For example, to find the shortest path from A to G:
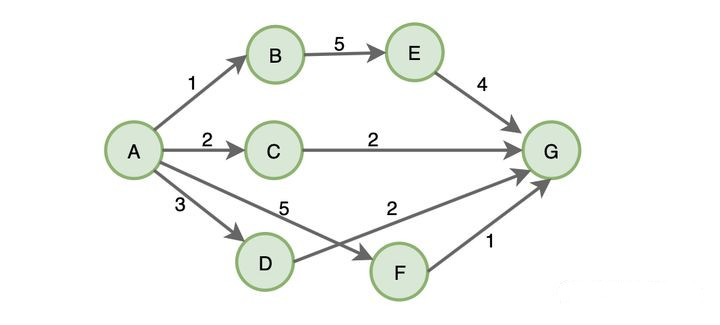
According to the greedy algorithm always choose the current optimal choice, so the first path it chooses is AB, then BE, EG, the total length of the path obtained is 1 + 5 + 4 = 10, however, this is not the shortest path, the shortest path is A->C->G : 2 + 2 = 4, so that the greedy algorithm is not necessarily the optimal solution.
So when can we try to use the greedy algorithm in general?
It can be used when the following conditions are met.
The complexity of the original problem is too high
The mathematical model for the global optimal solution is difficult to build or too computationally intensive
There is no great need to find the global optimal solution, “better” is fine
If the greedy algorithm is used to find the optimal solution, the following steps can be followed.
First, we need to specify what is the optimal solution (expectation)
Then, the problem is divided into multiple steps, each of which needs to satisfy the following.
Feasibility: each step satisfies the constraints of the problem
Local optimality: a locally optimal choice is made at each step
– Non-cancellable: once the choice is made, it cannot be cancelled in any subsequent situation
Finally, the optimal solution of all steps is superimposed, which is the global optimal solution
3.3 Classical example: Activity selection problem
The classical problems solved using the greedy algorithm are
Minimum spanning tree algorithm
Dijkstra’s algorithm for single source shortest path
Huffman compression coding
Backpacking problem
Activity selection problem, etc.
Among them, the activity selection problem is the simplest, and this is described in detail here.
The activity selection problem is an example from Introduction to Algorithms and is a very classical problem. There are n activities (a1,a2,…,an) that need to use the same resource (e.g., a classroom), and the resource can only be used by one activity at a given time. Each activity ai has a start time si and an end time fi. Once selected, activity ai occupies the half-open time interval [si,fi). If [si,fi) and [sj,fj) do not overlap with each other, both activities ai and aj can be scheduled for that day.
The problem is to schedule these events so that as many events as possible can be held without conflict. For example, the following figure shows a set S of activities, where the activities are ordered monotonically increasing by their ending times.
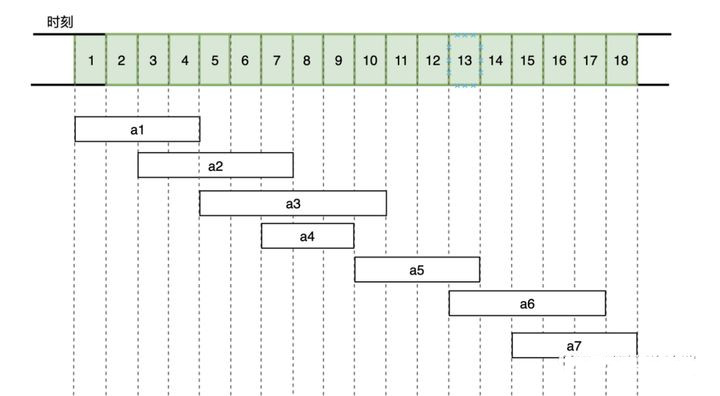
There are 7 activities that will take up the time in 18 hours as shown above. How can we choose the activities that will give the best utilization of this classroom (more activities can be held)?
The greedy algorithm has a simple solution to this kind of problem, it starts choosing at the beginning of the moment, and each time it chooses the activity whose start time does not conflict with the activity already chosen and whose end time is relatively close, so that the remaining time interval will be longer.
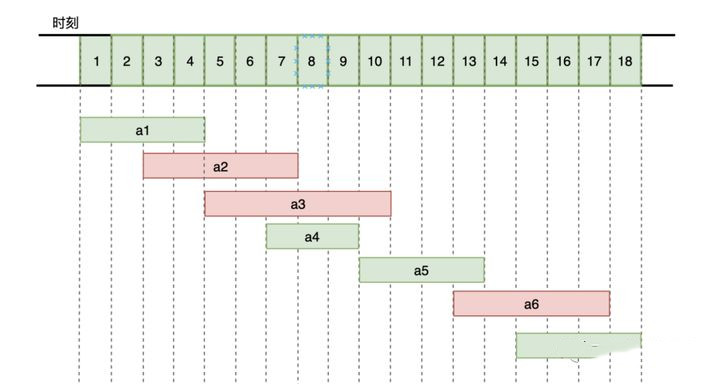
- a1 activity ends the earliest, choose a1 activity
- After a1 ends, a2 has a time conflict and cannot be selected. a3 and a4 can both be selected, but a4 has the earliest end time, select a4
- Select the activity with the earliest end time and no time conflict.
The final choice of activities a1, a4, a5, a7 is the optimal solution.