7.6 Longest palindromic substring
Given a string s, find the longest echo substring in s. You can assume that the maximum length of s is 1000.
Example 1.
Input: “babad”
Output: “bab”
Note: “aba” is also a valid answer.
Example 2.
Input: “cbbd”
Output: “bb”
Solution: Dynamic programming
Step 1: Define the state
dp[i][j] indicates whether the substring s[i..j] is a palindrome, where the substring s[i..j] is defined as a left-closed-right-closed interval that can be taken to s[i] and s[j].
Step 2: Think about the state transfer equation
For a substring, if it is a palindrome, then it is still a palindrome by adding an identical character to its first and last
dp[i][j] = (s[i] === s[j]) && dp[i+1][j-1]
Step 3: Initial state.
dp[i][i] = true // a single character is a palindrome
if(s[i] === s[i+1]) dp[i][i+1] = true // two consecutive identical characters are palindromes
Code implementation.
const longestPalindrome = (s) => {
if (s.length < 2) return s
// res: longest palindrome
let res = s[0], dp = []
for (let i = 0; i < s.length; i++) {
dp[i][i] = true
}
for (let j = 1; j < s.length; j++) {
for (let i = 0; i < j; i++) {
if (j – i === 1 && s[i] === s[j]) {
dp[i][j] = true
} else if (s[i] === s[j] && dp[i + 1][j – 1]) {
dp[i][j] = true
}
// Get the current longest echo substring
if (dp[i][j] && j – i + 1 > res.length) {
res = s.substring(i, j + 1)
}
}
}
return res
}
Complexity analysis.
Time complexity: O(n^2^)
Space complexity: O(n^2^)
More Answers
7.7 Minimal Path Sum
Given an m x n grid containing non-negative integers, find a path from the top left corner to the bottom right corner such that the sum of the numbers on the path is minimal.
Note: You can only move down or to the right one step at a time.

Example 1.
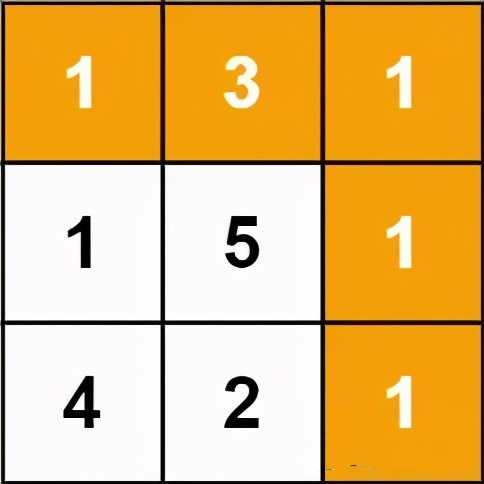
Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the sum of paths 1→3→1→1→1→1 is the smallest.
Example 2.
Input: grid = [[1,2,3],[4,5,6]]
Output: 12
Hint.
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 100
1, DP equation current term minimum path sum = current term value + minimum value in upper or left term grid[i][j] += Math.min( grid[i – 1][j], grid[i][j – 1] )
2, boundary processing grid’s first row and the first column do not have the upper term and the left term respectively, so a separate process to calculate the minimum path and calculate the first row.
for(let j = 1; j < col; j++) grid[0][j] += grid[0][j – 1]
Calculate the first column.
for(let i = 1; i < row; i++) grid[i][0] += grid[i – 1][0]
3. Code implementation
var minPathSum = function(grid) {
let row = grid.length, col = grid[0].length
// calc boundary
for(let i = 1; i < row; i++)
// calc first col
grid[i][0] += grid[i – 1][0]
for(let j = 1; j < col; j++)
// calc first row
grid[0][j] += grid[0][j – 1]
for(let i = 1; i < row; i++)
for(let j = 1; j < col; j++)
grid[i][j] += Math.min(grid[i – 1][j], grid[i][j – 1])
return grid[row – 1][col – 1]
};
More answers
7.8 The best time to buy and sell stocks II
Given an array, the i-th element is the price of a given stock on day i.
Design an algorithm to calculate the maximum profit you can make. You can complete as many trades as possible (multiple trades of a stock).
Note: You cannot participate in more than one trade at the same time (you must sell the previous stock before buying it again).
Example 1:
Input: [7,1,5,3,6,4]
Output: 7
Explanation: Buy on day 2 (stock price = 1) and sell on day 3 (stock price = 5), for a profit of = 5-1 = 4.
Subsequently, buy on day 4 (stock price = 3) and sell on day 5 (stock price = 6), for a profit of = 6-3 = 3.
Example 2:
Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (stock price = 1) and sell on day 5 (stock price = 5), the profit from this trade = 5-1 = 4.
Note that you cannot buy stocks on day 1 and day 2 back-to-back and then sell them later.
Because you are involved in multiple transactions at the same time, you must sell the previous shares before buying them again.
Example 3:
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no trade is completed, so the maximum profit is 0.
Tip.
1 <= prices.length <= 3 * 10 ^ 4
0 <= prices[i] <= 10 ^ 4
Solution 1: Buy at the bottom of the peak and sell at the top
Solution two: greedy algorithm
Greedy algorithm, as the name implies, always make the current optimal choice, that is, the expectation of the best local choice to obtain the best overall choice.
In a sense, the greedy algorithm is very greedy, very short-sighted, it does not consider the whole, only focus on the current maximum benefit, so that it makes the choice is only a sense of the local optimal, but the greedy algorithm in many problems can still get the optimal solution or better solution, so its existence is still meaningful.
Corresponding to the problem, buy on the first day, sell on the second day, …, buy on the i-th day, sell on the i+1-th day, buy if there is a profit from buying on the i-th day and selling on the i+1-th day, otherwise do not buy
buy on day i-1 and sell on day i for profit prices[i+1]-prices[i], we just need to add up all the positive values of prices[i+1]-prices[i] to get the maximum profit
Code implementation.
let maxProfit = function(prices) {
let profit = 0
for (let i = 0; i < prices.length – 1; i++) {
if (prices[i + 1] > prices[i]) {
profit += prices[i + 1] – prices[i]
}
}
return profit
}
Complexity analysis.
Time complexity: O(n)
Space complexity: O(1)
7.9 Distribute cookies
Let’s say you are a wonderful parent and want to give your children some small cookies. However, you can only give a maximum of one cookie per child. For each child i, there is an appetite value g~i~, which is the minimum size of cookie that will satisfy the children’s appetite; and for each cookie j, there is a size s~j~. If s~j~ >= g~i~ , we can assign this cookie j to child i and this child will be satisfied. Your goal is to satisfy as many children as possible, and output this maximum value.
Note that.
You can assume that the appetite value is positive. A child can have at most one cookie.
Example 1:
Input: [1,2,3], [1,1]
Output: 1
Explanation:
You have three children and two cookies. The appetite values of the three children are: 1,2,3.
Although you have two small cookies, since they are all of size 1, you can only satisfy the child whose appetite value is 1.
So you should output 1.
Example 2:
Input: [1,2], [1,2,3]
Output: 2
Explanation:
You have two children and three small cookies, two children with appetite values of 1,2 respectively.
You have enough number and size of cookies to satisfy all the children.
So you should output 2.
Solution: Greedy algorithm
const findContentChildren = (g, s) => {
if (!g.length || !s.length) return 0
g.sort((a, b) => a – b)
s.sort((a, b) => a – b)
let gi = 0, si = 0
while (gi < g.length && si < s.length) {
if (g[gi] <= s[si++]) gi++
}
return gi
}
More Answers
7.10 Splitting an array into consecutive subsequences
Given an array of integers num (which may contain repeated numbers) sorted in ascending order, divide them into one or more subsequences, each of which consists of consecutive integers and is at least 3 in length.
If you can do this, return true; otherwise, return false.
Example 1.
Input: [1,2,3,3,4,5]
Output: True
Explanation:
You can split two consecutive subsequences like this :
1, 2, 3
3, 4, 5
Example 2.
Input: [1,2,3,3,4,4,5,5]
Output: True
Explanation:
You can split two consecutive subsequences like this :
1, 2, 3, 4, 5
3, 4, 5
Example 3.
Input: [1,2,3,4,4,5]
Output: False
Tip.
The length of the input array is in the range [1, 10000].
Solution: Greedy algorithm
Starting from the beginning, we only look for sequences that satisfy the condition (consecutive subsequences of length 3) at a time, and after eliminating them, we iterate backwards in order.
determine whether the current element can be spliced to the previous contiguous subsequence that satisfies the condition, and if so, then splice
If not, determine whether the current element can form a consecutive subsequence (length 3), and if so, reject the consecutive subsequence
Otherwise, return false
const isPossible = function(nums) {
let max = nums[nums.length – 1]
// arr: stores the number of times each number appears in the original array
// tail: store the number of consecutive subsequences that end with the number num and match the question
let arr = new Array(max + 2).fill(0),
tail = new Array(max + 2).fill(0)
for(let num of nums) {
arr[num] ++
}
for(let num of nums) {
if(arr[num] === 0) continue
else if(tail[num-1] > 0){
tail[num-1]–
tail[num]++
}else if(arr[num+1] > 0 && arr[num+2] > 0){
arr[num+1] —
arr[num+2] —
tail[num+2]++
} else {
return false
}
arr[num]–
}
return true
}
Complexity analysis.
Time complexity: O(n)
Space complexity: O(n)
More Answers
7.11 Full permutation problem
Given a sequence of numbers with no repetitions, return all possible permutations.
Example:
Input: [1,2,3]
Output:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1], [3,2,1]
]
Solution: Backtracking algorithm
This problem is a classic application scenario of backtracking algorithm
1. Algorithm strategy
The backtracking algorithm is a search method, a trial method, which will make a choice at each step, and once it finds that this choice does not yield the desired result, it goes back and makes the choice again. Depth-first search uses the idea of backtracking algorithm.
2. Applicable scenarios
The backtracking algorithm is very simple, it just keeps trying until it gets the solution. This algorithmic idea makes it commonly used to solve breadth search problems, i.e., to select a solution that satisfies the requirements from a set of possible solutions.
3. Code implementation
We can write that the full permutation of the array [1, 2, 3] has.
first write the full permutations starting with 1, which are: [1, 2, 3], [1, 3, 2], i.e., the full permutation of 1 + [2, 3].
Then write the full permutations starting with 2, which are: [2, 1, 3], [2, 3, 1], i.e. the full permutation of 2 + [1, 3].
The last full permutations written starting with 3 are: [3, 1, 2], [3, 2, 1], i.e., the full permutation of 3 + [1, 2].
That is, the idea of backtracking is somewhat similar to enumeration search. We enumerate all the solutions and find the solution that satisfies the expectation. In order to enumerate all possible solutions in a regular manner and avoid omissions and repetitions, we divide the process of problem solving into multiple stages. At each stage, we face a fork in the road, and when we find that this road does not work (does not meet the desired solution), we backtrack to the previous fork and choose another way to go.
This is clearly a recursive structure.
The recursion terminates when enough numbers have been chosen in an alignment, so we need a variable to indicate how many levels of the recursion we are currently on.
used(object): used to indicate whether a number is selected, if the number (num) is selected this is set to used[num] = true, so that when considering the next position, you can determine whether the number has been selected in O(1) time complexity, which is a “space for time” idea.
let permute = function(nums) {
// Use an array to hold all possible permutations
let res = []
if (nums.length === 0) {
return res
}
let used = {}, path = []
dfs(nums, nums.length, 0, path, used, res)
return res
}
let dfs = function(nums, len, depth, path, used, res) {
// All the numbers are filled in
if (depth === len) {
res.push([.. .path])
return
}
for (let i = 0; i < len; i++) {
if (!used[i]) {
// dynamically maintain the array
path.push(nums[i])
used[i] = true
// continue recursively filling in the next number
dfs(nums, len, depth + 1, path, used, res)
// undo the operation
used[i] = false
path.pop()
}
}
}
4. Complexity analysis
Time complexity: O(n∗n!), where n is the length of the sequence This is a permutation, and the number of permutations per layer is: A^m^ ~n~=n!/(n-m)! , so all permutations have : A^1^ ~n~ + A^2^ ~n~ + … + A^n-1^ ~n~ = n!/(n-1)! + n!/(n-2)! + … + n! = n! * (1/(n-1)! + 1/(n-2)! + … + 1) <= n! * (1 + 1/2 + 1/4 + … + 1/2^n-1^) < 2 * n! and each internal node cycles n times, so the time complexity of non-leaf nodes is O(n∗n!)
Space complexity: O(n)
7.12 Parenthesis Generation
The number n represents the number of pairs of parentheses to generate. Design a function that can generate all possible and valid combinations of parentheses.
Example.
Input: n = 3
Output: [
“((())))”,
“(()()))”,
“(())()”,
“()((()))”,
“()()()()”
]
Solution: Backtracking algorithm (depth-first traversal)
Algorithm strategy: Backtracking algorithm is a search method, a trial method, which will make a choice at each step and once it finds that this choice does not yield the desired result, it goes back and makes the choice again. Depth-first search utilizes the backtracking algorithm idea.
Corresponding to this question, we can add ( or ) at each trial, noting that
The condition for adding ( is whether there is still ( available for selection
When adding (, it is restricted by (, if the ( in the selected result is less than or equal to the ) in the selected result, then it is not possible to select ), for example, if the current is (), continuing to select ) is ()), which is not legal.
Code implementation.
const generateParenthesis = (n) => {
const res = []
const dfs = (path, left, right) => {
// Definitely not legal, end early
if (left > n || left < right) return
// end condition reached
if (left + right === 2 * n) {
res.push(path)
return
}
// Select
dfs(path + ‘(‘, left + 1, right)
dfs(path + ‘)’, left, right + 1)
}
dfs(”, 0, 0)
return res
}