95% of all algorithms are based on these 6 algorithmic ideas(2)

4. backtracking algorithm
4.1 Algorithm strategy
The backtracking algorithm is a search method, a trial method, which will make a choice at each step, and once it finds that this choice does not yield the desired result, it goes back and makes the choice again. Depth-first search utilizes the idea of backtracking algorithm.

4.2 Application Scenarios
The backtracking algorithm is simple, it just keeps trying until it gets the solution. This algorithmic idea of it makes it commonly used to solve search problems of breadth, i.e., to select a solution that satisfies the requirements from a set of possible solutions.

4.3 Classic examples of using the backtracking algorithm
Depth-first search
0-1 backpacking problem
Regular expression matching
Eight Queens
Sudoku
Full alignment
etc. We have already introduced depth-first search in the chapter on graphs, so here is an example of regular expression matching

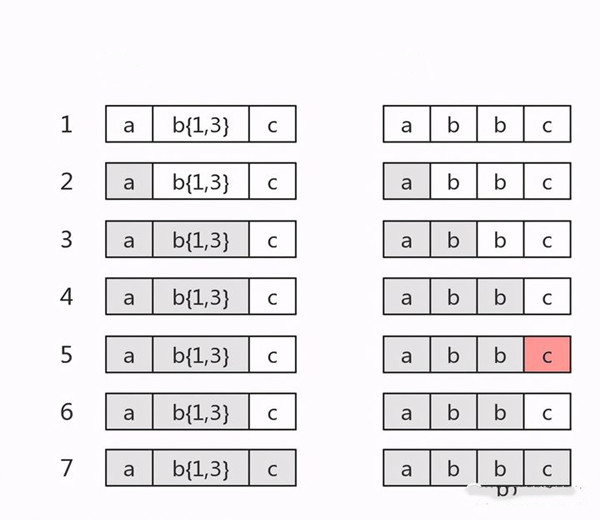
Regular expression matching
var string = “abbc”
var regex = /ab{1,3}c/
console.log( string.match(regex) )
// [“abbc”, index: 0, input: “abbc”, groups: undefined]
Its matching process

At step 5, b{1,3} has already matched two b’s and is trying for the third b. It turns out that c is next. At this point, we need to go back to the previous step, b{1,3} is matched (match to bb), and then match to c. Matching to c is finished.

5 Dynamic Planning
5.1 Algorithmic strategy
Unlike the partitioning algorithm, which requires the subproblems to be independent of each other, dynamic programming requires the subproblems to be interrelated.

Therefore, dynamic programming is suitable for the case of overlapping subproblems, i.e., different subproblems have common sub-subproblems. In this case, the partitioning strategy will make a lot of unnecessary work, and it will repeatedly solve those common sub-subproblems, while dynamic programming will solve each sub-subproblem once and then save it in a table, and if it encounters a consistent problem, it can get both from the table, so it does not need to solve each It does not need to solve each sub-sub-problem, which avoids a lot of unnecessary operations.

5.2 Application Scenarios
Dynamic programming is suitable for solving optimal problems, for example, selecting any number of coins from 100 coins of variable denomination to make $10, and asking how to select the coins so that the final number of coins selected is the least and just enough to make $10. This is a typical dynamic programming problem. It can be divided into one subproblem (picking coins each time), each subproblem has a common subsubproblem (picking coins), the subproblems are interrelated (the total amount of coins picked cannot exceed $10), and the boundary condition is that the total amount of coins picked is $10.

For the above example, maybe you can also say that we can use the backtracking algorithm and keep trying, but the backtracking algorithm is using the solution with the solution breadth (the solution that satisfies the requirement). If we are using the backtracking algorithm, we need to try to find all the solutions that satisfy the condition and then find the optimal solution with a time complexity of O(2^n^), which is quite poor performance. Most problems that apply to dynamic programming can use the backtracking algorithm, but the time complexity of using the backtracking algorithm is just higher.

Finally, to summarize, we need to follow the following important steps when solving problems using dynamic programming.

Define subproblems
Implement the part of the sub-sub-problem that requires iterative execution to solve
Identify and solve for the boundary conditions
5.3 Some classic problems solved using dynamic programming
Stair Climbing Problem: Suppose you are climbing a stairway. You need n steps to reach the top of the building. You can climb 1 or 2 steps at a time. How many different ways can you climb to the top of the building?
Backpack problem: Given some resources (with total amount and value), given a backpack (with total capacity), fill the backpack with resources, the goal is to fill the backpack with more value without exceeding the total capacity
Coin change: given a certain amount of change of variable denomination, and the number of money to be changed, find out how many change options there are
All-source shortest path of graph: a graph contains u, v vertices, find the shortest path from vertex u to vertex v
Longest common subsequence: find the longest common subsequence of a set of sequences (can be achieved by removing elements from another sequence but not changing the order of the remaining elements)
Here is an example of the longest common subsequence.

Stair Climbing Problem
Here is an example of the classical problem of dynamic programming, the stair climbing problem, to introduce the steps of solving dynamic programming problems.

Step 1: Define the subproblem

If dp[n] denotes the number of solutions for the nth step, and from the question: the last step may be 2 steps or 1 step, i.e., the number of solutions for the nth step is equal to the number of solutions for the n-1st step plus the number of solutions for the n-2nd step

Step 2: Implement the part of the sub-sub-problem that requires iterative execution to solve

dp[n] = dp[n-1] + dp[n-2]
Step 3: Identify and solve for the boundary conditions

// Level 0 1 solution
dp[0] = 1
// Level 1 is also 1 solution
dp[1]=1
Final step: translate the tail code into code to handle some boundary cases

let climbStairs = function(n) {
let dp = [1, 1]
for(let i = 2; i <= n; i++) {
dp[i] = dp[i – 1] + dp[i – 2]
}
return dp[n]
}
Complexity analysis.

Time complexity: O(n)
Space complexity: O(n)
Optimized space complexity.

let climbStairs = function(n) {
let res = 1, n1 = 1, n2 = 1
for(let i = 2; i <= n; i++) {
res = n1 + n2
n1 = n2
n2 = res
}
return res
}
Space complexity: O(1)

6 Enumeration Algorithm
6.1 Algorithm strategy
The idea of the enumeration algorithm is to enumerate all possible answers to the problem, and then determine whether the answer is suitable according to the conditions, keeping the suitable ones and discarding the unsuitable ones.

6.2 Problem Solving Ideas
Determine the enumeration object, the enumeration range, and the judgment condition.
Enumerate the possible solutions one by one and verify that each solution is the solution to the problem.
7 Brushing Problems
7.1 Stair Climbing Problem
Suppose you are climbing a flight of stairs. You need n steps to reach the top of the building.

You can climb 1 or 2 steps at a time. How many different ways can you climb to the top of the building?

Note: Given n is a positive integer.

Example 1.

Input: 2
Output: 2
Explanation: There are two ways to get to the top of the building.
1. 1 step + 1 step
2. 2 steps
Example 2.

Input: 3
Output: 3
Explanation: There are three ways to climb to the top of the building.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 orders + 1 order
Solution: Dynamic Programming
Dynamic Programming (DP) is a strategy for decomposing a complex problem into smaller problems, but unlike partitioning algorithms, which require that the subproblems be independent of each other, dynamic programming subproblems are interrelated.

Partitioning, as the name implies, is a divide and conquer, dividing a complex problem into two or more similar subproblems, and dividing the subproblem into smaller subproblems until the smaller subproblem can be solved simply by solving the subproblem, then the solution of the original problem is the merging of the subproblem solutions.
When we use dynamic programming to solve a problem, we need to follow the following important steps.

Define the subproblem
Implement the part of the sub-sub-problem that requires iterative execution of the solution
Identify and solve for the boundary conditions
Step 1: Define the subproblem

If dp[n] denotes the number of solutions for the nth step, and by the title: the last step can be 2 steps or 1 step, i.e., the number of solutions for the nth step is equal to the number of solutions for the n-1st step plus the number of solutions for the n-2nd step

Step 2: Implement the part of the sub-sub-problem that requires iterative execution to solve

dp[n] = dp[n-1] + dp[n-2]
Step 3: Identify and solve for the boundary conditions

// Level 0 1 solution
dp[0] = 1
// Level 1 is also 1 solution
dp[1]=1
Final step: translate the tail code into code to handle some boundary cases

let climbStairs = function(n) {
let dp = [1, 1]
for(let i = 2; i <= n; i++) {
dp[i] = dp[i – 1] + dp[i – 2]
}
return dp[n]
}
Complexity analysis.

Time complexity: O(n)
Space complexity: O(n)
Optimized space complexity.

let climbStairs = function(n) {
let res = 1, n1 = 1, n2 = 1
for(let i = 2; i <= n; i++) {
res = n1 + n2
n1 = n2
n2 = res
}
return res
}
Space complexity: O(1)

More Answers

7.2 Climbing Stairs Using Minimum Cost
Each index of the array is a ladder, and the i-th ladder corresponds to a non-negative number of stamina cost[i] (indexes start at 0).

Each time you climb a ladder you spend the corresponding stamina cost, and then you can choose to climb one more ladder or two more.

You need to find the minimum cost to reach the top of the floor. At the beginning, you can choose the element with index 0 or 1 as the initial ladder.

Example 1:

Input: cost = [10, 15, 20]
Output: 15
Explanation: The minimum cost starts at cost[1] and then takes two steps to the top of the ladder, for a total cost of 15.
Example 2:

Input: cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
Output: 6
Explanation: The minimum cost is 6, starting from cost[0] and going through the 1’s one by one, skipping cost[3].
Note that

The length of cost will be in [2, 1000].
Each cost[i] will be an Integer of type [0, 999].
Solution: Dynamic Programming
This problem is based on the following idea.

The i-th step is the top of the i-1st step.
It costs cost[i] to step on the i-th step, but it costs nothing to take a big step without stepping on it.
The top of the stairs is outside the array, and if the length of the array is len, then the top of the stairs is outside the array with subscript len
Step 1: Define the subproblem

The physical effort to step up the i-th step is the minimum physical effort to reach the first two steps plus the physical effort at this level.

Last 1 step to step i: dp[i-1] + cost[i]
last 1 step on step i: dp[i-2] + cost[i]
Step 2: Implement the part of the sub-sub-problem that requires iterative execution to solve

So the minimum cost to take the i-th step is

dp[i] = min(dp[i-2], dp[i-1]) + cost[i]
Step 3: Identify and solve for the boundary conditions

// Level 0 cost[0] scenario
dp[0] = cost[0]
// Level 1, there are two cases
// 1: step on level 0 and level 1 respectively, cost[0] + cost[1]
// 2: two steps from the ground directly to the first step, cost[1]
dp[1] = min(cost[0] + cost[1], cost[1]) = cost[1]
Final step: translate the tail code into code that handles some boundary cases

let minCostClimbingStairs = function(cost) {
cost.push(0)
let dp = [], n = cost.length
dp[0] = cost[0]
dp[1] = cost[1]
for(let i = 2; i < n; i++){
dp[i] = Math.min(dp[i-2] , dp[i-1]) + cost[i]
}
return dp[n-1]
}
Complexity analysis.

Time complexity: O(n)
Space complexity: O(n)
Optimization.

let minCostClimbingStairs = function(cost) {
let n = cost.length,
n1 = cost[0],
n2 = cost[1]
for(let i = 2;i < n;i++){
let tmp = n2
n2 = Math.min(n1,n2)+cost[i]
n1 = tmp
}
return Math.min(n1,n2)
};
Time complexity: O(n)
Space complexity: O(1)
More Answers

7.3 Maximum Subsequence Sum
Given an array of integers nums, find a contiguous subarray with a maximum sum (the subarray contains at least one element) and return its maximum sum.

Example:

Input: [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: The sum of successive subarrays [4,-1,2,1] is the largest, which is 6.
Advanced:

If you have already implemented a solution with O(n) complexity, try to use a more subtle partitioning method.

Step 1: Define the subproblem

Dynamic programming considers the entire array inductively. Suppose we already know the maximum sum of consecutive subarrays ending with the i-1st number, dp[i-1]. Obviously the possible values of the maximum sum of consecutive subarrays ending with the i-th number are either dp[i-1]+nums[i] or nums[i] in a separate group, that is, nums[i], where we take the maximum of the two numbers.

Step 2: Implement the part of the sub-sub-problem that requires iterative execution to solve

dp[n] = Math.max(dp[n-1]+nums[n], nums[n])
Step 3: Identify and solve for the boundary conditions

dp[0]=nums[0]
Final step: translate the tail code into code and handle some boundary cases

Since we only care about dp[i-1] and nums[i] when computing dp[i], we don’t need to save the whole dp array, just set a pre to save dp[i-1].

Code implementation (optimization).

let maxSubArray = function(nums) {
let max = nums[0], pre = 0
for(const num of nums) {
if(pre > 0) {
pre += num
} else {
pre = num
}
max = Math.max(max, pre)
}
return max
}
Complexity analysis.

Time complexity: O(n)
Space complexity: O(1)
More Answers

7.4 The best time to buy and sell stocks
Given an array, its i-th element is the price of a given stock on the i-th day.

If you are allowed to complete at most one trade (i.e., buy and sell a stock once), design an algorithm to calculate the maximum profit you can make.

Note: You cannot sell a stock before you buy it.

Example 1:

Input: [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (stock price = 1) and sell on day 5 (stock price = 6), maximum profit = 6-1 = 5.
Note that the profit cannot be 7-1 = 6, because the sell price needs to be greater than the buy price; also, you cannot sell the stock before buying it.
Example 2:

Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no trade is completed, so the maximum profit is 0.
Solution: Dynamic programming
Step 1: Define the subproblem

Suppose we already know that the maximum profit of i-1 stocks is dp[i-1], and obviously the maximum profit of i consecutive stocks is dp[i-1], which is either prices[i] – minprice (minprice is the minimum value of the first i-1 stocks), or we take the maximum of these two numbers

Step 2: Implement the part of the sub-sub-problem that requires iterative execution to solve

dp[i] = Math.max(dp[i-1], prices[i] – minprice)
Step 3: Identify and solve for the boundary conditions

dp[0] = 0
Final step: translate the tail code into code to handle some boundary cases

Since we only care about dp[i-1] and prices[i] when computing dp[i], instead of saving the whole dp array, just set a max to save dp[i-1].

Code implementation (optimization).

let maxProfit = function(prices) {
let max = 0, minprice = prices[0]
for(let i = 1; i < prices.length; i++) {
minprice = Math.min(prices[i], minprice)
max = Math.max(max, prices[i] – minprice)
}
return max
}
Complexity analysis.

Time complexity: O(n)
Space complexity: O(1)
More Answers

7.5 Palindromic substrings
Given a string, your task is to calculate how many palindromic substrings are in this string.

Substrings with different start positions or end positions are treated as different substrings, even if they consist of the same characters.

Example 1.

Input: “abc”
Output: 3
Explanation: Three palindromic substrings: “a”, “b”, “c”
Example 2.

Input: “aaa”
Output: 6
Explanation: 6 iambic substrings: “a”, “a”, “a”, “aa”, “aa”, “aaa”, “aaa”
Tip.

The length of the input string will not exceed 1000 .
Solution 1: Brute force method
let countSubstrings = function(s) {
let count = 0
for (let i = 0; i < s.length; i++) {
for (let j = i; j < s.length; j++) {
if (isPalindrome(s.substring(i, j + 1))) {
count++
}
}
}
return count
}

let isPalindrome = function(s) {
let i = 0, j = s.length – 1
while (i < j) {
if (s[i] ! = s[j]) return false
i++
j–
}
return true
}
Complexity analysis.

Time complexity: O(n^3^)
Space complexity: O(1)
Solution 2: Dynamic programming
A string is a palindrome, it has the same first and last characters and the remaining substring is also a palindrome. Where, whether the remaining substring is a palindrome or not is the smaller subproblem, and its result affects the result of the larger problem.

How do we describe the subproblem?

Obviously, a substring identified by the i , j pointers at each end is the variable that describes the subproblem, the substring s[i.. .j] (dp[i][j]) is the subproblem whether it is a palindrome or not.

We use a two-dimensional array to record the results of the computed subproblems, and recurse the solution of each subproblem from the base case, like filling a table.

j
a a b a
i a ✅
a ✅
b ✅
a ✅
Note: i<=j , using only half a table, scanning vertically

So.

i === j: dp[i][j] = true
j – i == 1 && s[i] == s[j]: dp[i][j] = true
j – i > 1 && s[i] == s[j] && dp[i + 1][j – 1]: dp[i][j] = true
That is.

s[i] == s[j] && (j – i <= 1 || dp[i + 1][j – 1]): dp[i][j] = true
otherwise false

Code implementation.

let countSubstrings = function(s) {
const len = s.length
let count = 0
const dp = new Array(len)

for (let i = 0; i < len; i++) {
dp[i] = new Array(len).fill(false)
}
for (let j = 0; j < len; j++) {
for (let i = 0; i <= j; i++) {
if (s[i] == s[j] && (j – i <= 1 || dp[i + 1][j – 1])) {
dp[i][j] = true
count++
} else {
dp[i][j] = false
}
}
}
return count
}
Code implementation (optimization).

Consider the vertical column of the table above as a one-dimensional array, still scanned vertically, at this point you just need to define dp as a one-dimensional array

let countSubstrings = function(s) {
const len = s.length
let count = 0
const dp = new Array(len)

for (let j = 0; j < len; j++) {
for (let i = 0; i <= j; i++) {
if (s[i] === s[j] && (j – i <= 1 || dp[i + 1])) {
dp[i] = true
count++
} else {
dp[i] = false
}
}
}
return count;
}
Complexity analysis.

Time complexity: O(n^2^)
Space complexity: O(n)